The unit circle with tangent values is a fundamental concept in trigonometry that plays a crucial role in understanding the relationships between angles and their trigonometric functions. Whether you're a student, educator, or someone curious about mathematics, mastering this topic can open doors to advanced studies in calculus, physics, and engineering. The unit circle serves as a visual tool that simplifies the understanding of sine, cosine, and tangent functions, making it easier to solve complex problems.
Trigonometry is not just about memorizing formulas; it’s about understanding the underlying principles that govern the behavior of angles and their relationships. The unit circle, with its radius of 1, provides a standardized framework for analyzing these relationships. By incorporating tangent values into the unit circle, we can explore how the tangent function behaves across different quadrants and angles.
In this article, we will delve deep into the unit circle with tangent values, breaking down its components, applications, and significance. We’ll also explore how this concept is used in real-world scenarios, supported by examples, diagrams, and references to authoritative sources. By the end of this guide, you’ll have a solid grasp of the unit circle and its tangent values, empowering you to tackle trigonometric challenges with confidence.
Read also:Unlocking Convenience A Complete Guide To Vancouver Clinic Mychart App
Table of Contents
- What is the Unit Circle?
- Understanding Tangent Values
- Unit Circle Diagram with Tangent Values
- Behavior of Tangent in Different Quadrants
- Applications of Tangent in Real Life
- How to Calculate Tangent Values
- Common Angles and Their Tangent Values
- Solving Problems Using the Unit Circle
- Frequently Asked Questions
- Conclusion
What is the Unit Circle?
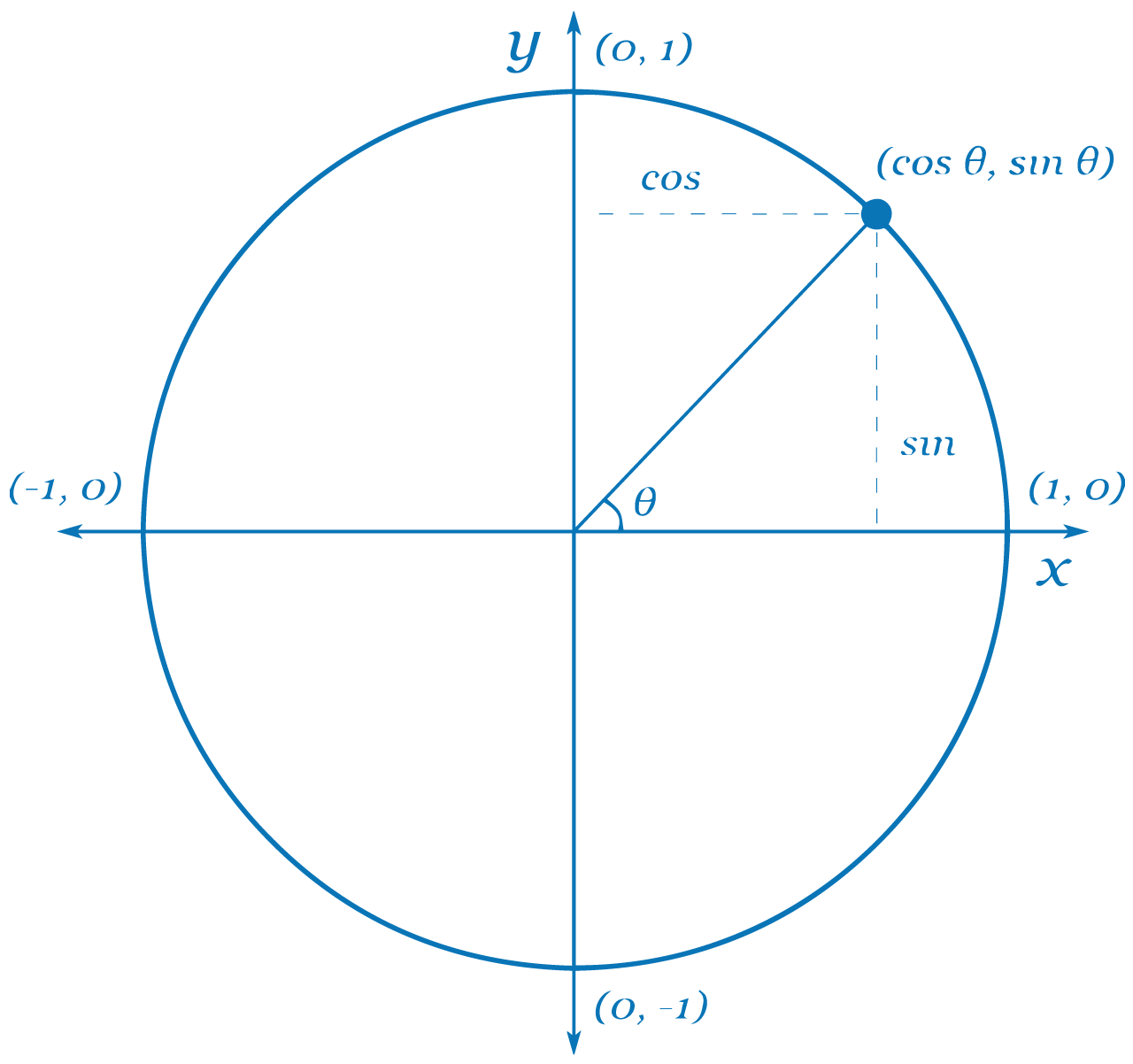
The unit circle is a circle with a radius of 1, centered at the origin (0, 0) in the Cartesian coordinate system. It is a powerful tool in trigonometry because it allows us to visualize the relationships between angles and their trigonometric functions, such as sine, cosine, and tangent. The equation of the unit circle is given by:
\[ x^2 + y^2 = 1 \]
This equation represents all points (x, y) that lie on the circle. Each point on the circle corresponds to a specific angle measured in radians or degrees, starting from the positive x-axis and moving counterclockwise.
Why is the Unit Circle Important?
- It simplifies the calculation of trigonometric functions.
- It provides a visual representation of angles and their corresponding sine, cosine, and tangent values.
- It is used extensively in calculus, physics, and engineering to solve problems involving periodic functions.
By mastering the unit circle, you can solve trigonometric problems more efficiently and gain a deeper understanding of how angles relate to their functions.
Understanding Tangent Values
The tangent of an angle in the unit circle is defined as the ratio of the sine to the cosine of that angle:
\[ \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} \]
Read also:The Ultimate Guide To The Infatuation New York Discover The Citys Best Kept Secrets
This means that the tangent value depends on the sine and cosine values of the angle. Since the sine and cosine values are derived from the coordinates of a point on the unit circle, the tangent value can also be expressed as:
\[ \tan(\theta) = \frac{y}{x} \]
Key Properties of Tangent
- Tangent is undefined when the cosine of the angle is zero (i.e., when \( x = 0 \)).
- The tangent function is periodic with a period of \( \pi \) radians (180 degrees).
- It has vertical asymptotes where the cosine value is zero.
Understanding these properties is essential for interpreting tangent values on the unit circle.
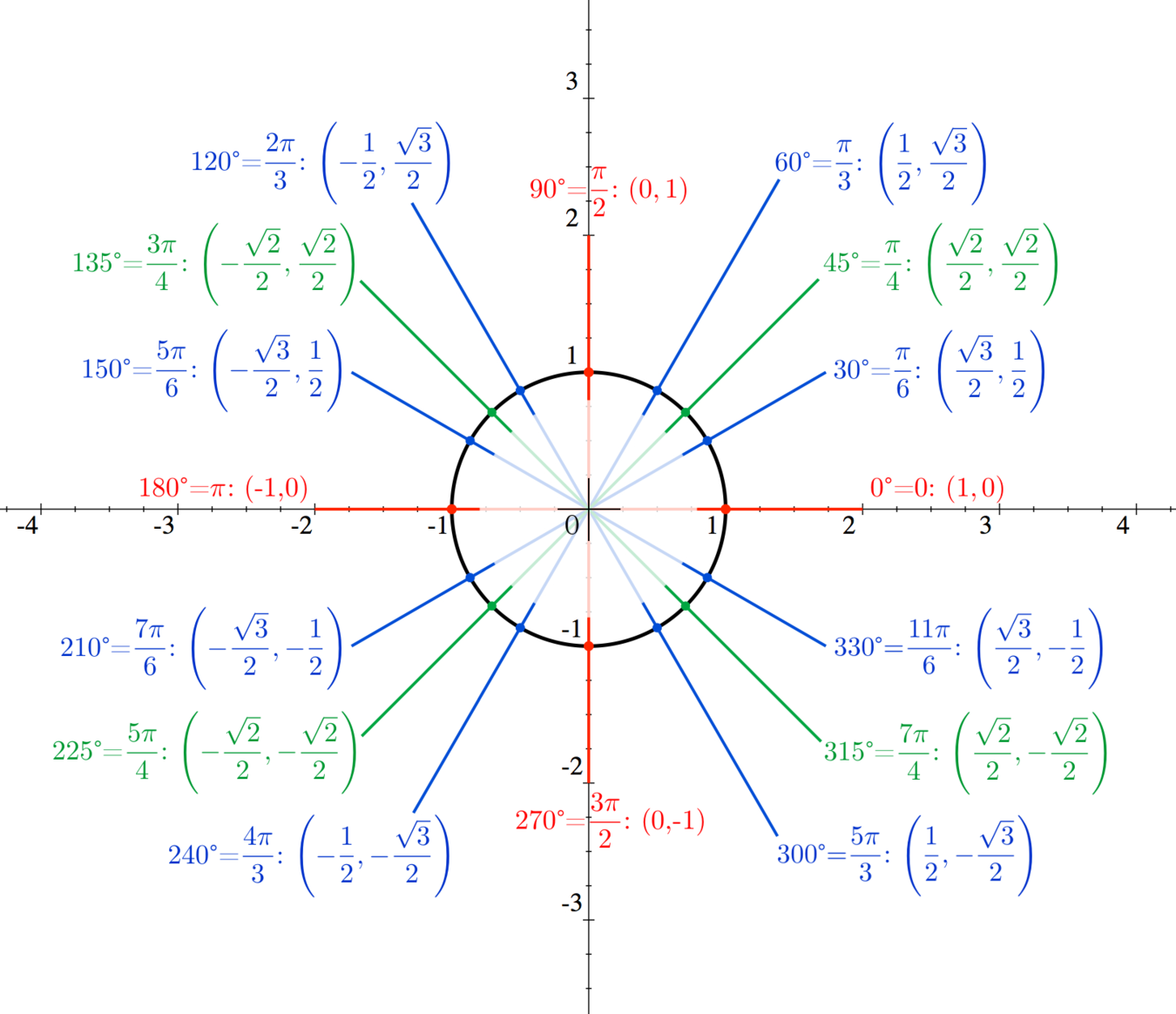
Unit Circle Diagram with Tangent Values
To better understand the unit circle with tangent values, let’s visualize it. Below is a description of the unit circle diagram:
- The circle is divided into four quadrants, each representing a range of angles.
- Angles are measured in radians (e.g., \( \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3} \)) and degrees (e.g., 30°, 45°, 60°).
- Each point on the circle corresponds to an angle and has coordinates (cosine, sine).
- Tangent values are calculated as \( \frac{\text{sine}}{\text{cosine}} \).
For example, at \( \frac{\pi}{4} \) radians (45°), the coordinates are \( \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) \), and the tangent value is 1.
Behavior of Tangent in Different Quadrants
The tangent function behaves differently in each quadrant of the unit circle. Let’s explore its behavior:
Quadrant I (0 to \( \frac{\pi}{2} \))
In Quadrant I, both sine and cosine values are positive, so the tangent value is also positive. For example:
- At \( \frac{\pi}{6} \), \( \tan(\frac{\pi}{6}) = \frac{\sqrt{3}}{3} \).
- At \( \frac{\pi}{4} \), \( \tan(\frac{\pi}{4}) = 1 \).
Quadrant II (\( \frac{\pi}{2} \) to \( \pi \))
In Quadrant II, sine is positive, and cosine is negative, resulting in a negative tangent value. For example:
- At \( \frac{2\pi}{3} \), \( \tan(\frac{2\pi}{3}) = -\sqrt{3} \).
Quadrant III (\( \pi \) to \( \frac{3\pi}{2} \))
In Quadrant III, both sine and cosine are negative, so the tangent value is positive. For example:
- At \( \frac{4\pi}{3} \), \( \tan(\frac{4\pi}{3}) = \sqrt{3} \).
Quadrant IV (\( \frac{3\pi}{2} \) to \( 2\pi \))
In Quadrant IV, sine is negative, and cosine is positive, resulting in a negative tangent value. For example:
- At \( \frac{5\pi}{3} \), \( \tan(\frac{5\pi}{3}) = -\frac{\sqrt{3}}{3} \).
Applications of Tangent in Real Life
The tangent function is not just a theoretical concept; it has numerous practical applications in various fields:
- Physics: Tangent is used to calculate the slope of a curve or the angle of inclination in mechanics.
- Engineering: Engineers use tangent values to design structures, such as bridges and buildings, ensuring stability and safety.
- Navigation: Pilots and sailors use tangent to determine angles and distances for navigation.
- Computer Graphics: Tangent values are used in rendering 3D models and animations.
These applications highlight the importance of understanding the unit circle with tangent values in real-world contexts.
How to Calculate Tangent Values
Calculating tangent values involves using the sine and cosine values of an angle. Here’s a step-by-step guide:
- Identify the angle in radians or degrees.
- Find the sine and cosine values of the angle using the unit circle or a calculator.
- Divide the sine value by the cosine value to get the tangent value.
For example, at \( \frac{\pi}{3} \) radians (60°):
- \( \sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2} \)
- \( \cos(\frac{\pi}{3}) = \frac{1}{2} \)
- \( \tan(\frac{\pi}{3}) = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3} \)
Common Angles and Their Tangent Values
Below is a table of common angles and their corresponding tangent values:
| Angle (Radians) | Angle (Degrees) | Tangent Value |
|---|---|---|
| 0 | 0° | 0 |
| \( \frac{\pi}{6} \) | 30° | \( \frac{\sqrt{3}}{3} \) |
| \( \frac{\pi}{4} \) | 45° | 1 |
| \( \frac{\pi}{3} \) | 60° | \( \sqrt{3} \) |
| \( \frac{\pi}{2} \) | 90° | Undefined |
Solving Problems Using the Unit Circle
Let’s solve a few problems to reinforce your understanding of the unit circle with tangent values:
Problem 1: Find \( \tan(\frac{5\pi}{6}) \)
1. Locate \( \frac{5\pi}{6} \) on the unit circle (Quadrant II).
2. Find the sine and cosine values: \( \sin(\frac{5\pi}{6}) = \frac{1}{2} \), \( \cos(\frac{5\pi}{6}) = -\frac{\sqrt{3}}{2} \).
3. Calculate the tangent value: \( \tan(\frac{5\pi}{6}) = \frac{\frac{1}{2}}{-\frac{\sqrt{3}}{2}} = -\frac{\sqrt{3}}{3} \).
Problem 2: Solve \( \tan(\theta) = 1 \)
1. Identify the angles where \( \tan(\theta) = 1 \): \( \theta = \frac{\pi}{4}, \frac{5\pi}{4} \).
2. Verify using the unit circle.
Frequently Asked Questions
Q: What happens when the tangent value is undefined?
A: The tangent value is undefined when the cosine value is zero, which occurs at \( \frac{\pi}{2} \) and \( \frac{3\pi}{2} \).
Q: Why is the unit circle important for tangent values?
A: The unit circle provides a standardized framework for visualizing and calculating tangent values for any angle.
Q: Can tangent values be negative?
A: Yes, tangent values can be negative in Quadrants II and IV, where sine and cosine have opposite signs.
Conclusion
The unit circle with tangent values is an indispensable tool in trigonometry, offering a clear and concise way